Maths- Gym for Brainiacs
+30
Ion Creanga
alexander mahone
El Gunner
Dutti
mr-r34
urbaNRoots
forza.milan
vizkosity
Forza
ausbaz
TheRedStag
fatman123
Baraa
Ganso
beatrixasdfghjk.
Rossoneri Ninja
kiranr
spanky
halamadrid2
BiasedMilanFan3
Sushi Master
EarlyPrototype
Jack Daniels
RealGunner
Lord Hades
S
Soul
dansik
Ali
Babun
34 posters
Goal Legacy :: The Hub :: Archive
Page 20 of 27
Page 20 of 27 •  1 ... 11 ... 19, 20, 21 ... 23 ... 27
1 ... 11 ... 19, 20, 21 ... 23 ... 27 
 Re: Maths- Gym for Brainiacs
Re: Maths- Gym for Brainiacs
fatman123 wrote:beatrixasdfghjk. wrote:How do you integrate a Lorenz curvevizkosity wrote:i'm ignorant when it comes to stats :[
integration is simply "the sum of values". It's not what people generally believe in-area under the curve. Though that might help, but during the third/2nd year of math, they will flush that idea out of your head..
heres a better question: how do you know what a Lorenz curve and that coefficent thing are? theres no way thats part of HSC economics
i don't even know what Lorenz curve is lol...i thought it was Lorentz's math for some reason...and wiki is just too much to read for me atm
vizkosity- First Team

- Posts : 1065
Join date : 2012-05-04
 Re: Maths- Gym for Brainiacs
Re: Maths- Gym for Brainiacs
Lorentz transformation?
 .
.
The Lorenz curve plots a cumulative increase of population against a cumulative increase in income, or something like that...
The Gini coefficient is given by the area between the Lorenz curve and the line of equality, divided by the entire area under the line of equality...
The Lorenz curve plots a cumulative increase of population against a cumulative increase in income, or something like that...
The Gini coefficient is given by the area between the Lorenz curve and the line of equality, divided by the entire area under the line of equality...
beatrixasdfghjk.- Fan Favorite

- Club Supported :

Posts : 5059
Join date : 2011-06-06
 Re: Maths- Gym for Brainiacs
Re: Maths- Gym for Brainiacs
math doesn't look that hard, but i have a hard time grasping terms....some are obvious, others are not. But it's the sum (sigma) turned integral with 2 endpoints (interval) that can estimate the number of

whatever the multiplication between the x and y axis yield?

whatever the multiplication between the x and y axis yield?

vizkosity- First Team

- Club Supported :

Posts : 1065
Join date : 2012-05-04
Age : 32
 Re: Maths- Gym for Brainiacs
Re: Maths- Gym for Brainiacs
beatrixasdfghjk. wrote:Yes it is, what the hell are you talking about...fatman123 wrote:beatrixasdfghjk. wrote:How do you integrate a Lorenz curvevizkosity wrote:i'm ignorant when it comes to stats :[
integration is simply "the sum of values". It's not what people generally believe in-area under the curve. Though that might help, but during the third/2nd year of math, they will flush that idea out of your head..
heres a better question: how do you know what a Lorenz curve and that coefficent thing are? theres no way thats part of HSC economics
It's under income inequality, as well as the effects of globalisation and all that stuff.
i didnt do HSC eco and ive never heard it mentioned, maybe ill cover it next semester in Macroeconomics

fatman123- Fan Favorite

- Club Supported :

Posts : 9616
Join date : 2011-06-06
Age : 30
 Re: Maths- Gym for Brainiacs
Re: Maths- Gym for Brainiacs
beatrixasdfghjk. wrote:Lorentz transformation?.
The Lorenz curve plots a cumulative increase of population against a cumulative increase in income, or something like that...
The Gini coefficient is given by the area between the Lorenz curve and the line of equality, divided by the entire area under the line of equality...
lorentz transformation is a heavy algebra (disgusting imo) that is closely related to einstein's special relativity work. It basically translate from frames to frames, as time is not the same in every frame. The same factors are called lorentz invariants. Ie, electric charge, q. But time, position x, and speed v can all be change after transforming
Hence, we have satellites that aren't miles off when giving signal to our GPS

vizkosity- First Team

- Club Supported :

Posts : 1065
Join date : 2012-05-04
Age : 32
 Re: Maths- Gym for Brainiacs
Re: Maths- Gym for Brainiacs
I haven't done integration yetvizkosity wrote:math doesn't look that hard, but i have a hard time grasping terms....some are obvious, others are not. But it's the sum (sigma) turned integral with 2 endpoints (interval) that can estimate the number of
whatever the multiplication between the x and y axis yield?
How would you get the equation of a Lorenz curve?
beatrixasdfghjk.- Fan Favorite

- Club Supported :

Posts : 5059
Join date : 2011-06-06
 Re: Maths- Gym for Brainiacs
Re: Maths- Gym for Brainiacs
beatrixasdfghjk. wrote:I haven't done integration yetvizkosity wrote:math doesn't look that hard, but i have a hard time grasping terms....some are obvious, others are not. But it's the sum (sigma) turned integral with 2 endpoints (interval) that can estimate the number of
whatever the multiplication between the x and y axis yield?.
How would you get the equation of a Lorenz curve?
y=mx+b


fatman123- Fan Favorite

- Club Supported :

Posts : 9616
Join date : 2011-06-06
Age : 30
 Re: Maths- Gym for Brainiacs
Re: Maths- Gym for Brainiacs
The Lorenz curve isn't a straight line  .
.
 .
.
beatrixasdfghjk.- Fan Favorite

- Club Supported :

Posts : 5059
Join date : 2011-06-06
 Re: Maths- Gym for Brainiacs
Re: Maths- Gym for Brainiacs
it's shown on wikipedia. Kinda hard to explain integration from a an infinite sum. However, i shall do it the conventional way. You might need as far as over 2 years of calculus to properly understand the math for the lorenz stuffs (not that complicated, but i figure u would need to know more than just geometric series  ).
).
Anyways, integrating is a sum of a function value between 2 points with infinite interval.

if you treat y as a point*, you will see that to obtain all the areas under the curve (which was taught in many calculus 1st year classes), you will need an infinite amount of x interval to be 100% certain (more blocks). However, Newton had figured out how to do it. It's basically the anti derivative, which says that acceleration = derivative of velocity = derivative of position x.
Derivatives are simply slope, or rate of change. They don't have to be constants, but they do follow strict rules. Integrals are harder, some are obvious, others can't never be figured (many still are), but they are simply...the sum of values* ( or area in many cases).
Why is it important? well...we know that a= dv/dt
and v = dx/dt
dt is with respect to time (x-axis).
so let's imagine we have a as a constant.
to find v, we simply have to integrate it...if you look at your graph with acceleration with respect to time, you will notice that the area will be m/s^2 * s = m/s, which is the unit of velocity!
the rule for polynomial is simple,
1 higher power for a and divide by that number of power.
v= at/1 (t because we integrate with respect to t). power is 1 now.
we tag on a V0 (initial velocity) to help clarify the arbitrary. We might decelerate, but god knows from how fast?!?
so v = at/1 +v0
now integrate again!
m/s *s = meter, the unit of position right?
x = (at^2)/2 +Vot/1 + Xo(arbitrary position again!)
x(t) = 0.5t^2 +Vot + Xo, which brings us to the ramos equation
let's give Xo = 0 (on ground), we can solve for the maximum height by taking the derivation (once again the slope!). At maximum height, it's a downward parabola shape, so slope at maximum = 0
from there, you can solve for t time it takes to reach max, and plug it in to find the maximum height!
now, back to our curve. If we assume that it's area under the curve, then we can simply find 2 integrals of those 2 functions (probably polynomials), and take the top one minus the bottom one (the area in the middle). That would give us the gini coefficient? (if i understand the concept correctly).

rule for poly
note that if u are integrating between 2 pts like our friend curves, then the arbitrary numbers will cancel out
Anyways, integrating is a sum of a function value between 2 points with infinite interval.

if you treat y as a point*, you will see that to obtain all the areas under the curve (which was taught in many calculus 1st year classes), you will need an infinite amount of x interval to be 100% certain (more blocks). However, Newton had figured out how to do it. It's basically the anti derivative, which says that acceleration = derivative of velocity = derivative of position x.
Derivatives are simply slope, or rate of change. They don't have to be constants, but they do follow strict rules. Integrals are harder, some are obvious, others can't never be figured (many still are), but they are simply...the sum of values* ( or area in many cases).
Why is it important? well...we know that a= dv/dt
and v = dx/dt
dt is with respect to time (x-axis).
so let's imagine we have a as a constant.
to find v, we simply have to integrate it...if you look at your graph with acceleration with respect to time, you will notice that the area will be m/s^2 * s = m/s, which is the unit of velocity!
the rule for polynomial is simple,
1 higher power for a and divide by that number of power.
v= at/1 (t because we integrate with respect to t). power is 1 now.
we tag on a V0 (initial velocity) to help clarify the arbitrary. We might decelerate, but god knows from how fast?!?
so v = at/1 +v0
now integrate again!
m/s *s = meter, the unit of position right?
x = (at^2)/2 +Vot/1 + Xo(arbitrary position again!)
x(t) = 0.5t^2 +Vot + Xo, which brings us to the ramos equation
let's give Xo = 0 (on ground), we can solve for the maximum height by taking the derivation (once again the slope!). At maximum height, it's a downward parabola shape, so slope at maximum = 0
from there, you can solve for t time it takes to reach max, and plug it in to find the maximum height!
now, back to our curve. If we assume that it's area under the curve, then we can simply find 2 integrals of those 2 functions (probably polynomials), and take the top one minus the bottom one (the area in the middle). That would give us the gini coefficient? (if i understand the concept correctly).

rule for poly
note that if u are integrating between 2 pts like our friend curves, then the arbitrary numbers will cancel out

vizkosity- First Team

- Club Supported :

Posts : 1065
Join date : 2012-05-04
Age : 32
 Re: Maths- Gym for Brainiacs
Re: Maths- Gym for Brainiacs
What's the difference between an antiderivative and a primitive?
beatrixasdfghjk.- Fan Favorite

- Club Supported :

Posts : 5059
Join date : 2011-06-06
 Re: Maths- Gym for Brainiacs
Re: Maths- Gym for Brainiacs
How do you eliminate the time variable?
beatrixasdfghjk.- Fan Favorite

- Club Supported :

Posts : 5059
Join date : 2011-06-06
 Re: Maths- Gym for Brainiacs
Re: Maths- Gym for Brainiacs



this is obviously your starting point.
where you have F on the horizontal axis and L on the vertical so basically you get the equation Y=L(X), with F being your X. now all u have to do is find out what S means.

spanky- First Team

- Club Supported :

Posts : 1442
Join date : 2011-06-05
Age : 34
 Re: Maths- Gym for Brainiacs
Re: Maths- Gym for Brainiacs
they don't use that term here, but as much as i can understand, it's the definite integral, or antiderivatives without boundary.beatrixasdfghjk. wrote:What's the difference between an antiderivative and a primitive?
http://www.bymath.com/studyguide/ana/sec/ana8.htm
Which means we tag on another C, constant. In this case, it was Vo, and Xo. Those are initial position and velocity
If they don't specify boundaries, the answer is a set of solution, not a number. Why? any C would make the equation right. Once again, we don't know if ramos started kicking the ball 3 feet above the ground or not. You can also think of it this way, if the ball arrives at the space station, we dont know if ramos kicked the ball while in orbit, or on the ground. Ofc he needs to kick harder if he was in front of Neuer :S
So yes, anything that arrives at the space station and orbit the earth at that certain radius CAN be right. However, if we specify the initial place with the intitial velocity at the right moment, we WILL only have 1 scenario....and ofc, he kicked it super hard while staring at Neuer :[ Because if he kicks it too hard while in orbit, the ball will not orbit the Earth at the radius of 3Rt
hope that makes sense

vizkosity- First Team

- Club Supported :

Posts : 1065
Join date : 2012-05-04
Age : 32
 Re: Maths- Gym for Brainiacs
Re: Maths- Gym for Brainiacs
Wait, I'm just reading that they're the same thing...
beatrixasdfghjk.- Fan Favorite

- Club Supported :

Posts : 5059
Join date : 2011-06-06
 Re: Maths- Gym for Brainiacs
Re: Maths- Gym for Brainiacs
a primative, according to that site, is an indefinite integral. There are also definite integrals (integrating within 2 points-boundary)
Definite integral tends to give a number, ramos' case
indefinitely integrals will give you a set of solution with a constant C at the end, it tends to be a function, instead of a numerical answer (we dont know where ramos kick the ball, or what was the initial velocity of the ball when it reached the space station example)
(we dont know where ramos kick the ball, or what was the initial velocity of the ball when it reached the space station example)
Definite integral tends to give a number, ramos' case
indefinitely integrals will give you a set of solution with a constant C at the end, it tends to be a function, instead of a numerical answer

vizkosity- First Team

- Club Supported :

Posts : 1065
Join date : 2012-05-04
Age : 32
 Re: Maths- Gym for Brainiacs
Re: Maths- Gym for Brainiacs
How about you solve the problem then  .
.
beatrixasdfghjk.- Fan Favorite

- Club Supported :

Posts : 5059
Join date : 2011-06-06
 Re: Maths- Gym for Brainiacs
Re: Maths- Gym for Brainiacs
http://en.wikipedia.org/wiki/Trapezium_rule
http://en.wikipedia.org/wiki/Simpson%27s_rule
here u have some numerical integration methods, which u can use to find the integral of a function you dont know, but u do need to know the values for each point x,y(x), u also need to know the step of integration which means by how much you are increasing x ---> x+h,y(x+h).
with a small enough step you can accurately approximate the value of the curves integral.
http://en.wikipedia.org/wiki/Simpson%27s_rule
here u have some numerical integration methods, which u can use to find the integral of a function you dont know, but u do need to know the values for each point x,y(x), u also need to know the step of integration which means by how much you are increasing x ---> x+h,y(x+h).
with a small enough step you can accurately approximate the value of the curves integral.

spanky- First Team

- Club Supported :

Posts : 1442
Join date : 2011-06-05
Age : 34
 Re: Maths- Gym for Brainiacs
Re: Maths- Gym for Brainiacs
Yay, moar maths 
The thread gets interesting

You could only leave it out if an interval is given.
Next question
topic: analysis
difficulty: easy
requirements: knowledge of partial derivation and maximum/ minimum
Prove
x + y + z = 1 => xy + yz + xz < 1/2
Additional question: is it true for all x, y, z ?
The winner will get the best Asian boobslip video ever

The thread gets interesting

You forgot +c, c bleongs to the elements of real numbers . There're no definite integrationsvizkosity wrote:
rule for poly
note that if u are integrating between 2 pts like our friend curves, then the arbitrary numbers will cancel out

You could only leave it out if an interval is given.
Next question
topic: analysis
difficulty: easy
requirements: knowledge of partial derivation and maximum/ minimum
Prove
x + y + z = 1 => xy + yz + xz < 1/2
Additional question: is it true for all x, y, z ?
The winner will get the best Asian boobslip video ever


Babun- Fan Favorite

- Club Supported :

Posts : 7221
Join date : 2011-06-05
 Re: Maths- Gym for Brainiacs
Re: Maths- Gym for Brainiacs
it was copied from a site, and it looked neat enough for the kid :[
C is for constant.
In U.S., they have definite integral, which is a basically integrating between 2 pt. Not sure if they use it in other countries, but yea....if they are between the 2 intervals, C would cancel out. However, one need to plug in the values
C is for constant.
In U.S., they have definite integral, which is a basically integrating between 2 pt. Not sure if they use it in other countries, but yea....if they are between the 2 intervals, C would cancel out. However, one need to plug in the values

vizkosity- First Team

- Club Supported :

Posts : 1065
Join date : 2012-05-04
Age : 32
 Re: Maths- Gym for Brainiacs
Re: Maths- Gym for Brainiacs
http://archives.math.utk.edu/visual.calculus/4/definite.1/

vizkosity- First Team

- Club Supported :

Posts : 1065
Join date : 2012-05-04
Age : 32
 Re: Maths- Gym for Brainiacs
Re: Maths- Gym for Brainiacs
beatrixasdfghjk. wrote:How about you solve the problem then.
it was 5am in the morning and i thought i would get some sleep b4 moving back to college today. However, i think i provided enough info and steps on the other thread to solve the problem?
just make sure you use the y component of V to find the maximum height. Vy in this case which i believe is cosine of theta (theta being with respect to the perpendicular line, not horizonatal)

vizkosity- First Team

- Club Supported :

Posts : 1065
Join date : 2012-05-04
Age : 32
 Re: Maths- Gym for Brainiacs
Re: Maths- Gym for Brainiacs
Steps?vizkosity wrote:beatrixasdfghjk. wrote:How about you solve the problem then.
it was 5am in the morning and i thought i would get some sleep b4 moving back to college today. However, i think i provided enough info and steps on the other thread to solve the problem?
just make sure you use the y component of V to find the maximum height. Vy in this case which i believe is cosine of theta (theta being with respect to the perpendicular line, not horizonatal)
I've never done a question like this before, I don't really get it yet...
beatrixasdfghjk.- Fan Favorite

- Club Supported :

Posts : 5059
Join date : 2011-06-06
 Re: Maths- Gym for Brainiacs
Re: Maths- Gym for Brainiacs
beatrixasdfghjk. wrote:Steps?
I've never done a question like this before, I don't really get it yet...


fatman123- Fan Favorite

- Club Supported :

Posts : 9616
Join date : 2011-06-06
Age : 30
 Re: Maths- Gym for Brainiacs
Re: Maths- Gym for Brainiacs
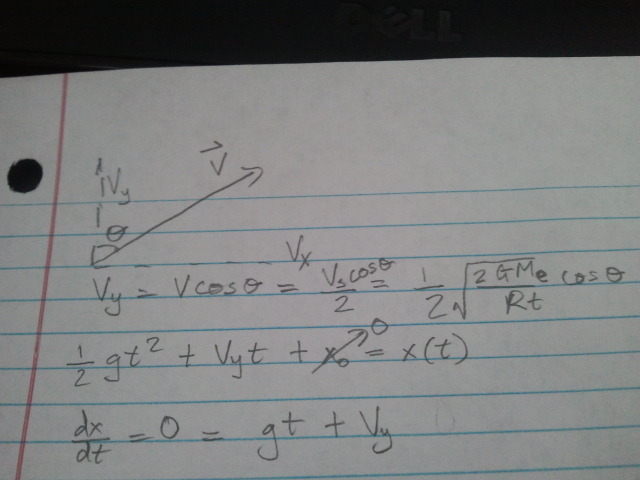
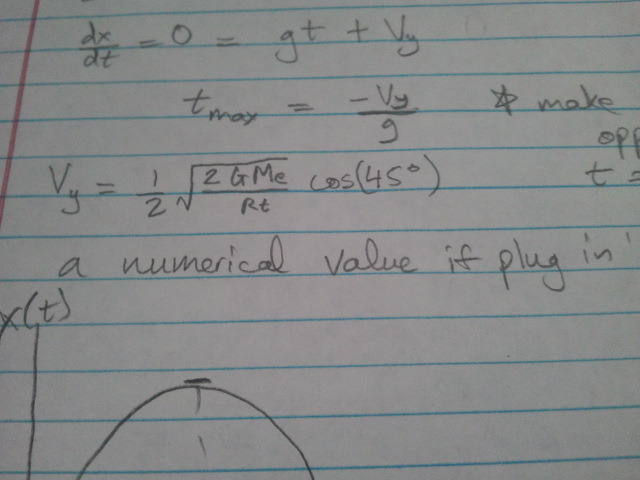


Vy points up, g points down, so tmax is "positive".
you don't need to know calculus to know where tmax is, the parabola graph has a vertex at -2b/a, which is basically -2(0.5Vy/g) = -Vy/g. Confirmed with the derivative.
At that time, the ball is instantaneously at rest (hence derivative of position = velocity = 0). I don't wanna plug in all the numbers, too lazy lol....but you can solve for Vy easily numerically, then find Tmax and eventually, as shown in the pic...d = Rt+ Xmax.
after obtaining d, just plug it in the last formula
hope this helps. Sorry, i was moving away from home once again and have to set up the internet, as well as unpack everything :[
Gravitational force is very straight forward. d is the distance from the center of mass (between the earth and the ball), but we'll assume that it is at the center of our Earth (almost the same thing can be say between our sun and the Earth).
Centripetal force is the force that makes everything goes in circle. Ie, as you swirl a ball tied to a string, it's the tension of the string that makes it goes in the circle (maybe + or - the gravity of Earth if you swirl it vertically.). Keep in mind that the only force acts on the ball now is the gravitational force (since it's in orbit.) The equation is then becomes Fg = Fc
Tell me if i make a mathematical error somewhere, I was rushing through it also.
Part b, comparing the radius of orbit of the ball vs. the space station, is very obvious. Just compare the number. The ball has less than the escape velocity, it will not fly forever. It will either orbit the earth, or fall back! It depends....if it orbits, which i'm guessing it will, or part b will be hard to answer, it will do so in a circle with a constant radius. If it falls back....well, it's always falling, but if it doesn't "miss" the earth as it moves sideway with a horizontal velocity, the will probably, never going to hit the space station.

vizkosity- First Team

- Club Supported :

Posts : 1065
Join date : 2012-05-04
Age : 32
 Re: Maths- Gym for Brainiacs
Re: Maths- Gym for Brainiacs
weve got ourselves a genius here 


spanky- First Team

- Club Supported :

Posts : 1442
Join date : 2011-06-05
Age : 34
 Re: Maths- Gym for Brainiacs
Re: Maths- Gym for Brainiacs
spanky489 wrote:weve got ourselves a genius here
it's just basic algebra :[
please don't embarrass me lol

vizkosity- First Team

- Club Supported :

Posts : 1065
Join date : 2012-05-04
Age : 32
Page 20 of 27 •  1 ... 11 ... 19, 20, 21 ... 23 ... 27
1 ... 11 ... 19, 20, 21 ... 23 ... 27 
Goal Legacy :: The Hub :: Archive
Page 20 of 27
Permissions in this forum:
You cannot reply to topics in this forum





» The US Politics Thread
» David Coote appreciation thread
» The Official Dwayne Wade <<<<<< you thread
» Soundtrack/Epic Music Appreciation Thread
» Leicester have sacked Claudio Ranieri
» Ruben Amorim Sack Watch
» Chillout Music!
» GL NBA fantasy 24-25
» The Music Room
» General Games Discussion
» Manchester United Part V / ETH Sack Watch
» The TV Series Thread - Part 5